我今天想分享一些个人比较喜欢的统计概念,其实相关的文章有不少,但我更希望简单明了点。
有关统计学在数据科学领域的重要性,在此就不过多赘述了。下面直接进入正题。
概率分布
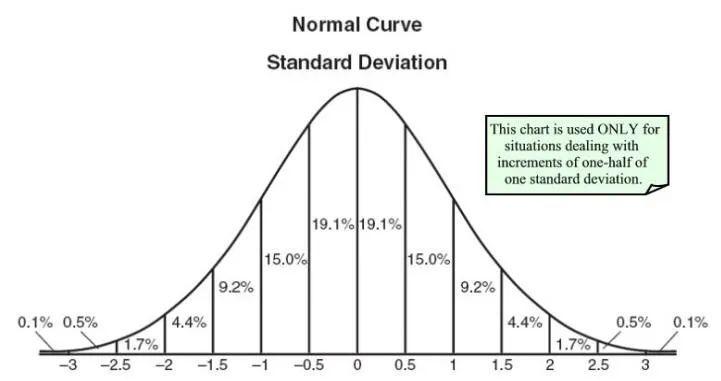
均匀分布只有一个值,且在特定范围内出现,该范围外的任何值都是0。我们可以把它看作是具有0或其他值的分类变量,但也依然可以把它想象成多个均匀分布的分段函数。
正态分布也被称为高斯分布,是由均值和标准差定义。均值在空间上移动分布,标准差控制分布程度。因此,我们会知道数据集的平均值和数据分布程度。
泊松分布和正态分布相似,但是增加了偏度。当偏态值较低时,它就会像正态分布一样在各个方向上的扩散相对均匀。而偏度值较高时,数据在不同方向上的扩散会有所不同。
当然,还有很多的分布你可以进行深入研究,但上述列出的3个已经为我们带来了价值,比如通过均匀分布,来解释分类数据;很多算法默认情况下可以很好的处理高斯分布;而在泊松分布中,我们必须格外小心并选择具有鲁棒性的算法。
过采样和欠采样
通常分类问题会使用。有时候,我们的分类数据集会偏向一侧。例如,对于类别1,我们有1000个样本,但是类别2就只有200个样本。在这种情况下,我们有两个预处理选项可以帮助训练机器学习模型。
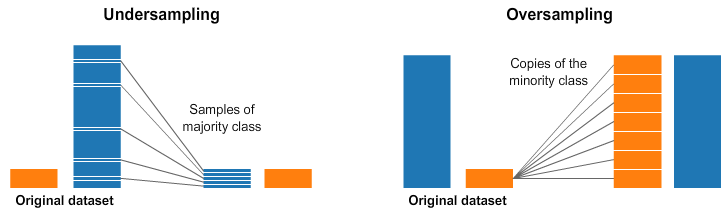
欠采样意味着我们需要从多数类别中选择一些数据,并且与少数类别的数目相同。这样就可以让采样后类别的概率分布取得平衡。这种方式就是通过选择更少的样本来保持数据集稳定。
过采样意味着我们创建少数类别的副本,以使其与多数类别相同。这种方式就是让数据集变得更均衡,并没有获得其他数据。
统计假设检验
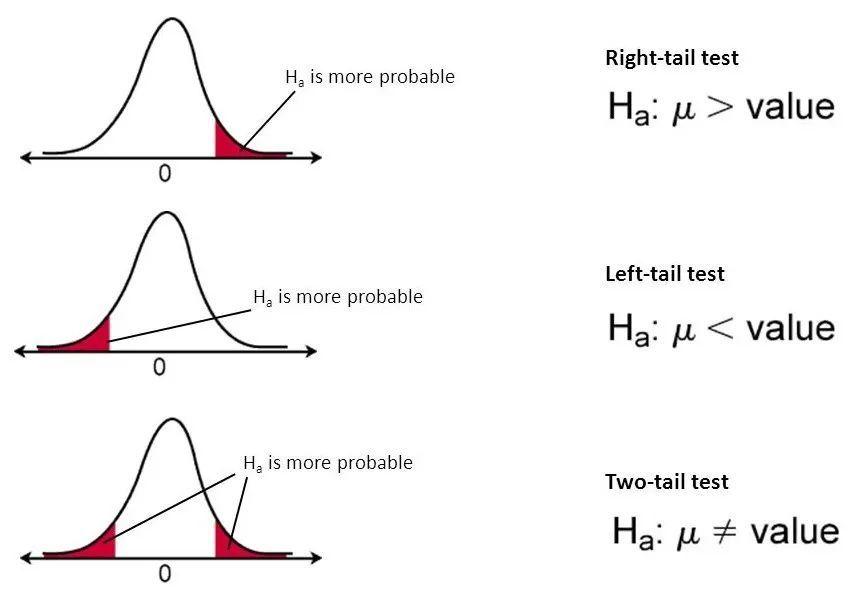
零假设:也称为原假设。
替代假设:确保研究没有缺陷的一种措施。
P值:它用来判定假设检验结果的一个参数。p值越小,意味着有更多的证据否定原假设。
Alpha:当原假设为真时否定它的概率,也称为1类错误。
Beta:称为2型错误,未能拒绝错误的原假设。
在所有统计概念中,这是我最喜欢的一个。假设检验是统计中必不可少的步骤,它有助于确定数据集的结果是否具有统计意义。
降维
这是减少数据集维度的过程,主要解决在高维数据集的情况下出现的问题。
根据下图,我们可以将数据集视为这个立方体结构,它具有三个维度和1000个点。
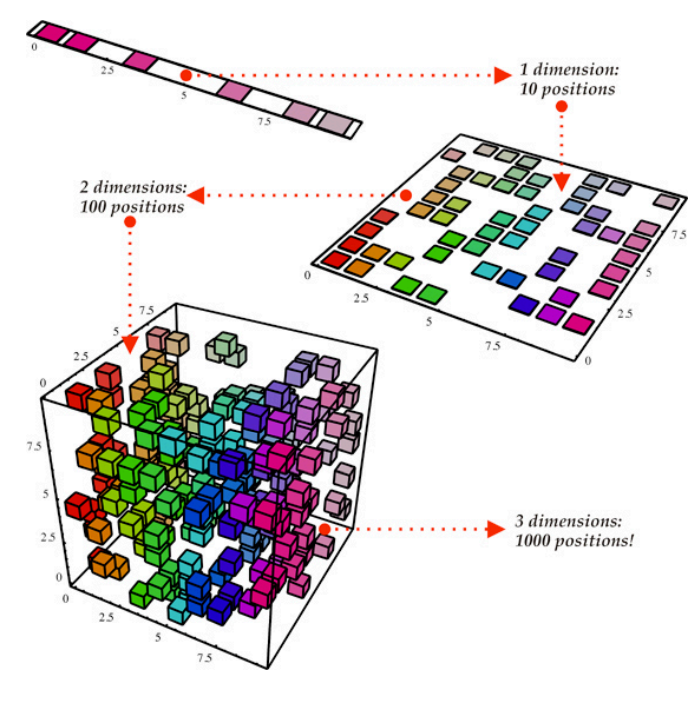
虽然现在来看,这个计算很容易,但在更大的范围时就可能遇到问题。
如果从多维数据集的一侧,以二维的角度看,可以很容易划分所有颜色。通过降维,可以将三维数据投射到二维平面上,这有效减少了需要计算的数量(最多100个)。
还有另一种方法——特征剪枝。用这种方式,可以删除对我们的分析不重要的特征。
例如,浏览数据集后,我们可能会发现9个独立变量,其中6个与输出的相关性很高,其他3个相关性就比较低,这样就可以在不会影响结果的情况下,考虑将它们删除。
降维里最常见的就是PCA,它是创建了影响相关输出的特征的向量表示。
结论
除了上述我所提到的,还有很多其他的统计概念,它们就像数据科学的基础,帮助解决现实中的一些复杂问题,让我们可以寻找到有意义的趋势和数据。所以,花足够的时间来学习这些会帮助提升技能。
来源:https://www.analyticsvidhya.com/blog/2020/11/top-5-favorite-statistical-concepts/,有所删减以及修改。
