我们都熟知“啤酒与尿布”的故事,但对其背后的算法却知之甚少。这个算法是什么?它可以帮助我们什么?这篇文章将进行解析。
提到Apriori算法,你可能对它并不熟悉。
但如果提到“啤酒与尿布”,你肯定知道或者多少听到过这个故事,美国沃尔玛超市的管理员分析销售数据时发现,在美国有婴儿的家庭中,父亲前往超市购买尿布时,通常也会顺便为自己买上啤酒。根据这个规律,超市将啤酒和尿布摆在同一个区域后,两个商品的销量都提升了。
一个现象的形成往往背后有更深层次的原因在推动。
“啤酒与尿布”两个看上去毫无关联的商品,通过购物篮分析挖掘出其中的关联性,获得了更多的销售机会。而在这种关联性分析里,Apriori算法可谓是入门但又最经典的算法。
那什么是Apriori算法?
从它的几个常见概念开始了解:支持度、置信度和频繁项集。
支持度
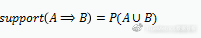
置信度
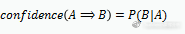
关联规则A⇒B的支持度support(A⇒B),表示A和B同时发生的概率,A⇒B的置信度confidence(A⇒B),表示在发生A的基础上发生B的概率。假如牛奶⇒面包的支持度support(A⇒B)=5%,置信度confidence(A⇒B)=40%,则说明在分析的购物数据中,5%的用户既买了牛奶又买了面包,在买了牛奶的所有用户中有40%的用户购买了面包。
频繁项集
项的集合称为项集,如果一个项集包含k个项,那么这个项集称为k项集。满足预定义的最小支持度阈值的项集,称为频繁项集,简单来说频繁项集就是在数据集中频繁出现的项集。频繁项集需要满足先验性质:频繁项集的所有非空子集也一定是频繁的。
关联分析中,挖掘关联规则的问题可以归结为挖掘频繁项集。Apriori算法使用一种称为逐层搜索的迭代方法,其中k项集用于探索(k+1)项集。
首先通过扫描数据库,累计每个项的计数,并收集满足最小支持度的项,找出频繁1项集的集合,计为L1。然后使用L1找出频繁2项集的集合L2,再使用L2找出L3,如此下去,直到不能再找到频繁k项集。
来看个例子
假设在数据库D中有5个购物车,购买的商品分别如下表所示:(设最小支持度计数为3):
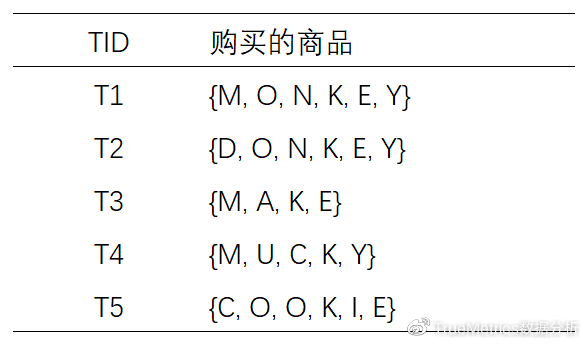
(1)首先,直接扫描D,对每个商品出现次数计数,得到:
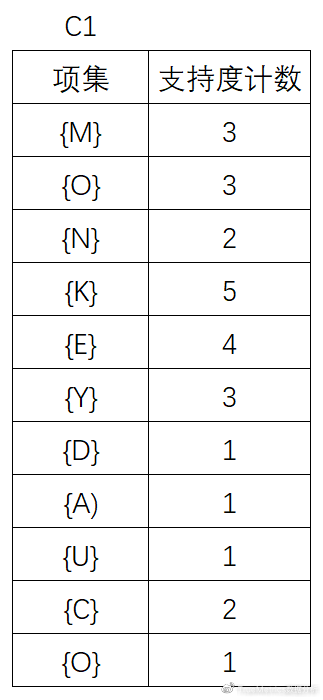
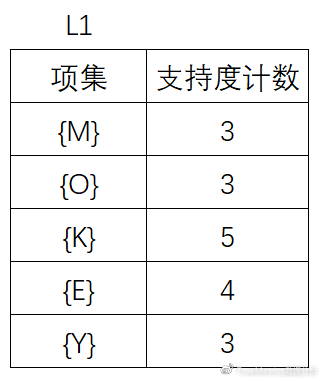
(2)将候选的支持度计数与最小支持度计数比较,去掉不满足最小支持度的项集,得到L1:

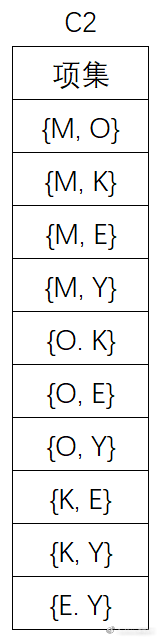
(4)扫描D,对C2中的每个候选项集的支持计数:
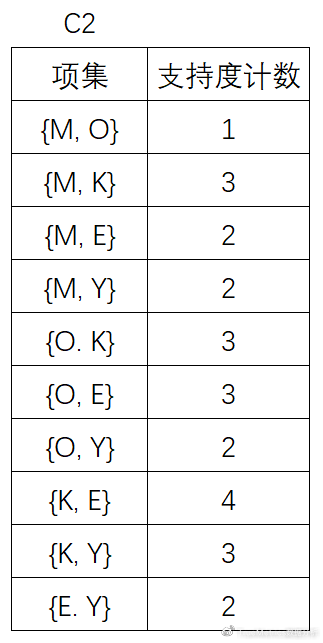
(5)将候选的支持度计数与最小支持度计数比较,去掉不满足最小支持度的项集,得到:
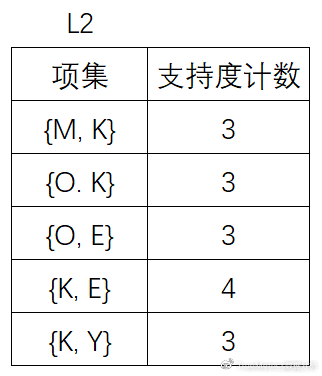


(7)扫描D,对C3中的每个候选项集的支持计数。另外根据先验性质,频繁项集的所有子集必须是频繁的,可以确定在C3中, {M, K, O} ,{M, K, E} ,{M, K, Y} ,{O, K, Y} ,{K, E, Y} 这4个候选不是频繁的,因此需要把它们从中去掉。
为什么这4个候选不是频繁的呢?
以{M, K, O}为例说明,{M, K, O}的子集{M, K}并未出现在L2中,子集{M, K}不是频繁的,所以{M, K, O}也不是频繁的
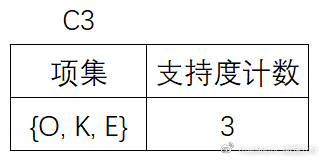
(8)将候选的支持度计数与最小支持度计数比较,去掉不满足最小支持度的项集,得到:
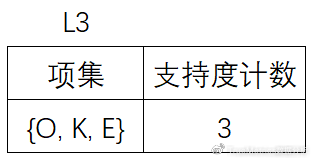
由于此时只剩一项,因此算法终止,找出了所有的频繁项集。在关联分析中,Apriori算法比较简单。可以帮助了解诸如“用户在一次会话中可能会同时浏览或购买哪些商品”类似的问题,并且能够将分析结果用于营销规划、广告投放、页面设计等方面。
举个例子,商超的布局通常会采取两种策略:一种策略是将经常同时购买的商品摆放在同一个区域,方便用户购买,或是进一步刺激这些商品的同时销售;另一种策略则是将经常同时购买的商品摆放在商店两端,以刺激购买这些商品的用户在沿途中去挑选其他商品。这就是基于关联分析设计出的“小心机”,来达到刺激用户购买的目的。
但是,Apriori算法也有一定的缺点,就是它可能需要产生大量的候选项集,而且需要重复的扫描整个数据库。
因此,后续又出现了另一种方法——频繁模式增长(Frequent-Pattern Growth),简称FP-growth,它可以用来发现频繁模式而不产生候选。但在今天的这篇文章中就不过多展开啦,留个小悬念,感兴趣的朋友可以留言交流~
